ワイブル分布を使って故障率分析してみた
信頼度工学の分野でワイブル分布を使って部品の故障率を求める方法を学んだので残しておこうと思います.
ワイブル分布とは*1
出どころ
ワイブル分布は,ある鎖を考えたときに,鎖の最も弱い部分が壊れることで鎖全体が壊れると考えた最弱リンクモデルと見なせます.
転じて,部品の劣化や寿命のモデルとして使われることが多いみたいです.
追記:
定義
ワイブル分布の確率密度関数PDF: ,累積分布関数CDF:
は以下で定義されます.
\begin{align}
f(x) &= \frac{\beta}{\alpha} \left( \frac{x}{\alpha} \right)^{\beta - 1} \exp \left[ - \left( \frac{x}{\alpha} \right)^{\beta} \right] \\
F(x) &= 1 - \exp \left[ - \left( \frac{x}{\alpha} \right)^{\beta} \right]
\end{align}
ここではワイブル係数(形状パラメータ),
は尺度パラメータと呼ばれます.
また,故障率というものを定義できます.
\begin{align}
\lambda (x) = \frac{f(x)}{1 - F(x)} = \frac{\beta}{\alpha ^ \beta} x^{\beta - 1}
\end{align}
故障率の定義は,を大きくして行ったとき,
\begin{align}
\lambda = \frac{x \mbox{ のとき故障する確率}}{\mbox{ある部品が}x\mbox{まで故障せず残っている確率}}
\end{align}
となっており,あるx時点で故障していない部品を集めて,その中の部品が故障する確率であると言えます.
私たちの持っている故障率のイメージと大体あっていますね.
手順
用いるデータ
まず架空のデータを用意しました.
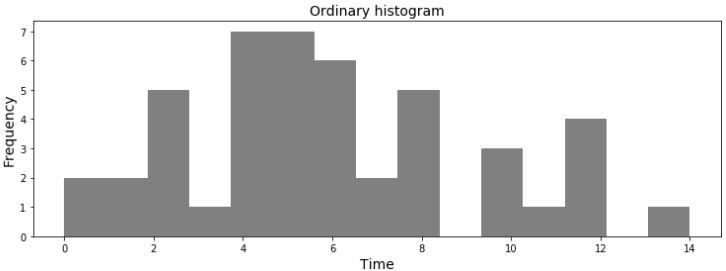
状況としては,ある部品を取り替えてから故障するまでの経過時間の記録が複数存在したのでヒストグラムにしてみた.という感じです.
つまり今回のワイブル分布の変数は (
:経過時間)ですね.
何がしたいのか
今回すべきことは,このデータに対して,適当なワイブル分布を当てはめることです.つまり,ワイブル分布において,変数を時間とすると,
\begin{align}
f(t) &= \frac{\beta}{\alpha} \left( \frac{t}{\alpha} \right)^{\beta - 1} \exp \left[ - \left( \frac{t}{\alpha} \right)^{\beta} \right]
\end{align}
中のを動かして,
がデータに最も適するような
を求めることに相当します.
その後求めたを用いて,故障率
\begin{align}
\lambda (t) = \frac{f(t)}{1 - F(t)} = \frac{\beta}{\alpha ^ \beta} t^{\beta - 1}
\end{align}
が決まるので,故障率と時間の関係から,故障の原因や部品をどの周期で交換すれば一番ベストなのか,等の考察ができます.
やってみよう
ワイブルプロット
ワイブル分布をデータにうまいこと当てはめる技をワイブルプロットというらしいので,ここでも使ってみましょう.
まず,ワイブル分布の累積分布関数CDFに着目します.
\begin{align}
F(t) &= 1 - \exp \left[ - \left( \frac{t}{\alpha} \right)^{\beta} \right]
\end{align}
ここで,先人が生み出した式変換を以下に紹介します.
\begin{align}
F(t) &= 1 - \exp \left[ - \left( \frac{t}{\alpha} \right)^{\beta} \right] \\
1 - F(t) &= \exp \left[ - \left( \frac{t}{\alpha} \right)^{\beta} \right] \\
\ln{ \left[ 1 - F(t) \right] } &= - \left( \frac{t}{\alpha} \right)^{\beta} \\
- \ln{ \left[ 1 - F(t) \right] } &= \left( \frac{t}{\alpha} \right)^{\beta} \\
\ln{ \left[ \frac{1}{1 - F(t)} \right] } &= \left( \frac{t}{\alpha} \right)^{\beta} \\
\ln{\left[ \ln{ \left[ \frac{1}{1 - F(t)} \right] } \right]} &= \beta \ln{t} - \beta \ln{\alpha} \\
\end{align}
これは
\begin{align}
Y &= a X + b \\
Y &= \ln{\left[ \ln{ \left[ \frac{1}{1 - F(t)} \right] } \right]} \\
X &= \ln{t} \\
a &= \beta \\
b &= - \beta \ln{\alpha}
\end{align}
の形のなっていますね.
つまり,ワイブル分布中のをデータから求めるときは,最小二乗法を使えば良いことがわかります.
最小二乗法に関しては,前回の記事
を参考にしてみてください.
まあ具体的にやってみましょう.
まずデータを累積確率に変換します
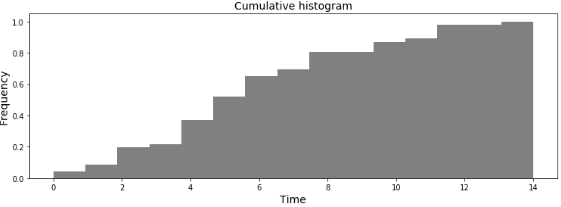
その後,このヒストグラムの縦軸F,横軸tを
\begin{align}
Y &= \ln{\left[ \ln{ \left[ \frac{1}{1 - F(t)} \right] } \right]} \\
X &= \ln{t} \\
\end{align}
に変換し,プロットし直します.
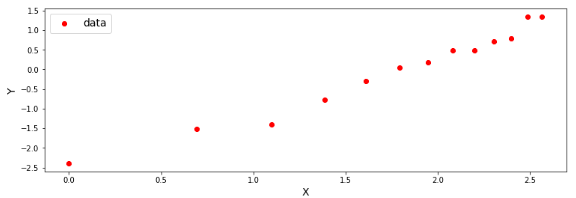
このデータに対して,最小二乗法を用いて,線を引くと...
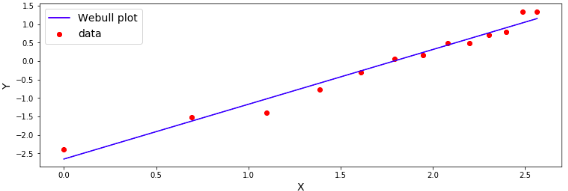
このように,一次関数が現れますね.この一次関数をワイブルプロットと呼びます.
こうして
\begin{align}
Y &= a X + b \\
a &= 1.48 \\
b &= -2.65
\end{align}
と求まったので,
\begin{align}
\beta &= a = 1.48 \\
\alpha &= \exp \left( -\frac{b}{\beta} \right) = 5.97
\end{align}
となります.
これでワイブル分布のパラメータが求まったので,データのヒストグラムに求めたワイブル分布を重ねてみましょう.
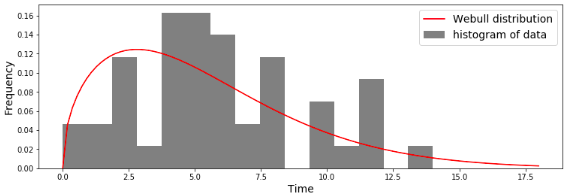
それっぽい形でワイブル分布が求まってますね.
故障率も出してみましょう.
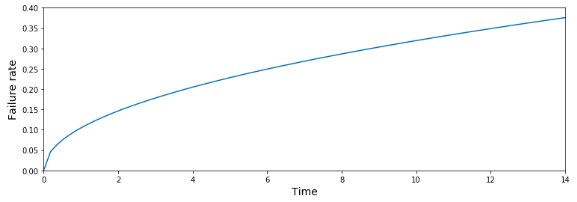
どうやら,部品は時間とともに故障率が高くなっていることがわかります.
このように,データにワイブル分布を仮定することで,部品の故障率の時間変化を推定することができました.
故障率について
故障率の定義
\begin{align}
\lambda (x) = \frac{f(x)}{1 - F(x)} = \frac{\beta}{\alpha ^ \beta} x^{\beta - 1}
\end{align}
をよく見ると,このグラフはが1を境に大きく形を変えることがわかります.
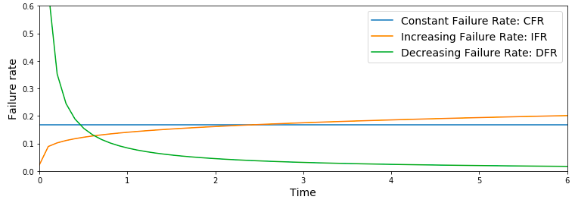
ここで,今回求めた故障率はIFRのグラフに該当することがわかります.これは摩耗型故障といって,時間とともに故障率は大きくなっていくパターンとなります.
DFRは初期不良型故障といって,初期に故障率が高いですが,初期不良がない場合故障率は下がっていくことがわかります.
CFRは偶発型故障といって,特に傾向はなく,一定の故障率をとります.
このように,ワイブル分布を仮定して,の大小を比較すれば,故障の原因が推定できて,対策を打つことができます.
例えば,
IFR型なら,早く交換する.
DFR型なら,早く交換しすぎるとまずいので,交換時期を長くする.
といった感じですね.
 のバラつきについて
のバラつきについて
の標準偏差は,Nを標本数として,
と知られています.
このバラつきを考慮して,グラフ化して見ると...
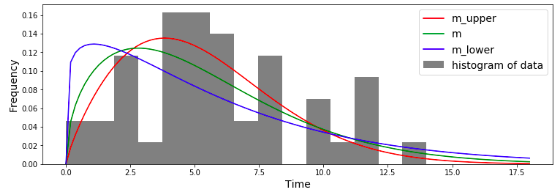

のようになります.この程度の標本数では,結構バラつくので,実際にワイブル分布を用いるときは注意したいですね.
まとめ
1.
ワイブル分布を用いることで,部品の故障の原因を推定するとともに,打つべき対策がわかる
2.
ワイブルプロットを行うことで,簡単にパラメータの推定が行うことができる.
3.
パラメータのバラつきも考慮して考察を行いましょう
Pythonで実際に行ったコードなどはまた今度まとめます...